Articles

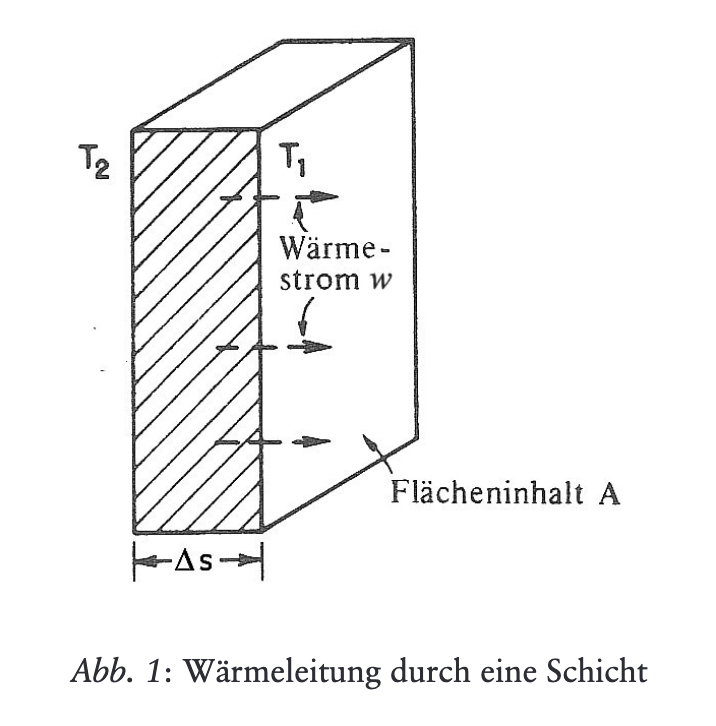
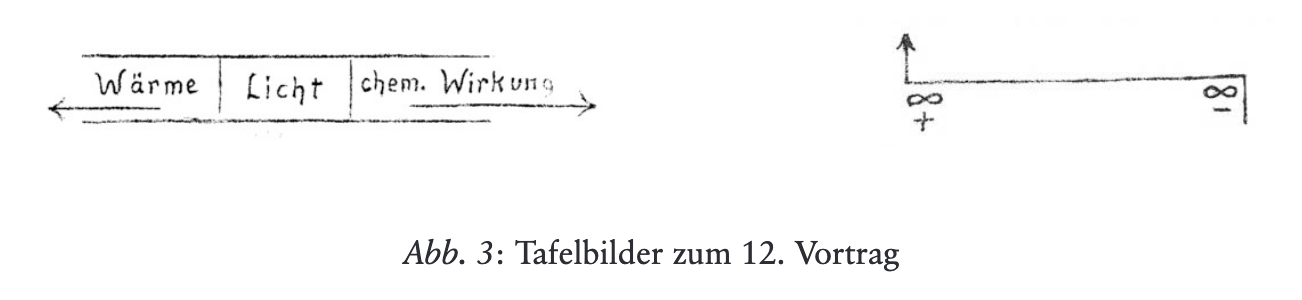
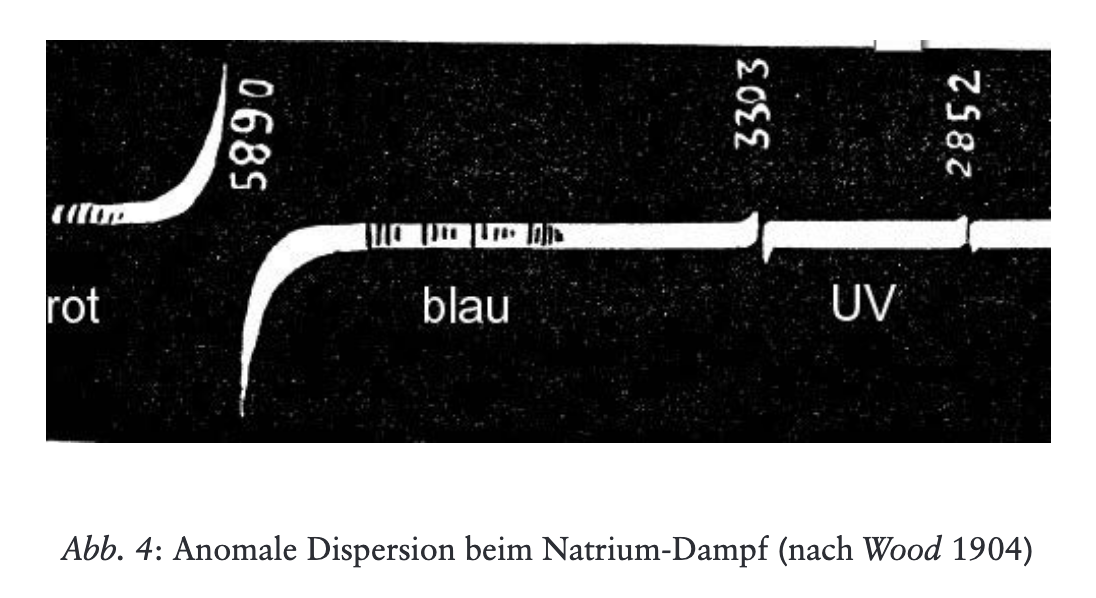
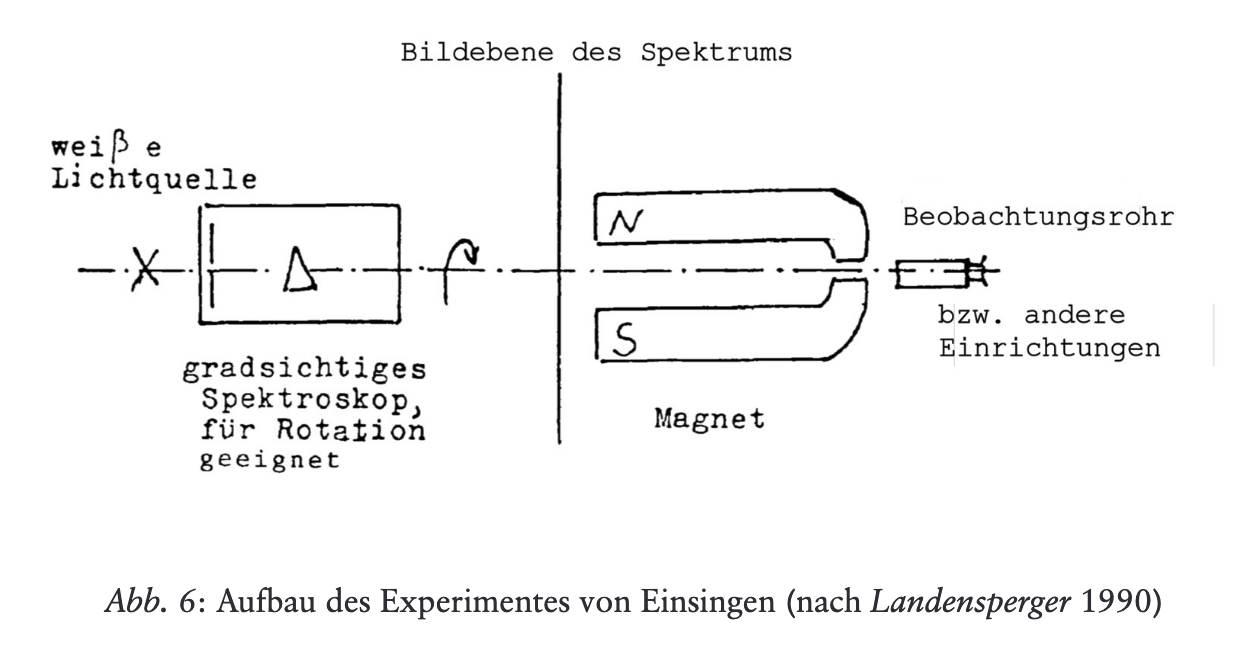
Die «Lichtleitungs»-Gleichung im 12. Vortrag des Wärmekurses

Friedrich-Wilhelm Dustmann
Elemente der Naturwissenschaft 117, 2022, P. 16-42 | DOI: 10.18756/edn.117.16
Article | Language: German | €6.00
Export Article Citation as

Abstract:

In the 12th lecture of Rudolf Steiner’s Warmth Course, in connection with the heat conduction equation, one finds two additional differential equations, the interpretation and application of which has been the subject of much speculation. The last of these equations is supposed to refer to light effects and is characterised by an imaginary coefficient and could therefore describe a diffusion process with an imaginary diffusion coefficient. Since the Schrödinger equation can also be interpreted in this way, the last equation has sometimes been seen as a kind of precursor to the Schrödinger equation. In this paper, it will be shown that the context in which the equation is found in the lecture series makes such an interpretation unlikely, since this context is mainly concerned with the light spectrum in connection with heat effects and chemical effects. A possibility is shown for how the conventional description of light propagation with the help of Maxwell’s equations can also be expressed by a differential equation with an imaginary or a complex light conduction coefficient, respectively.

References
  • Cadène, A., Berceau, P., Fouché, M., Battesti, R., Rizzo, C. (2013): Vacuum magnetic linear birefringence using pulsed fields: the BMV experiment. https://hal.archives-ouvertes.fr/hal-00793105v1
  • Dreher, E. (1882): Beiträge zu unserer modernen Atom- und Molekular-Theorie auf kritischer Grundlage. Halle.
  • Hardorp, D., Pinkall, U. (2000): Rudolf Steiner and Schrödinger’s equation, Math.-Phys. Korrespondenz 201, S. 16–22.
  • Josipovic, M. (2020): Geometric Mulriplication of Vectors – An Introduction to Geometric Algebra in Physics. Cham.
  • Kugler, W. (Hrsg.) (1987): Beiträge zur Rudolf Steiner Gesamtausgabe Nr. 95/96, Der Zwölffarbenkreis und eine Aufgabenstellung Rudolf Steiners zur Gewinnung von Lebensätherkräften aus dem Pfirsichblüt. Dornach.
  • Landensperger, W. (1990): Das Experiment von Einsingen, Elemente d. N. 52, S. 51–55.
  • Macdonald, A. (2021): Linear and Geometric Algebra. Wroclaw.
  • Pröbstl, A. (2002): Optische Aktivität von Kohlestoffverbindungen – Handeln und Erkennen im Wechsel, Elemente d. N. Sondernummer, S. 3–13.
  • Pohl, R.W. (1964): Mechanik, Akustik und Wärmelehre, 16. Aufl. Göttingen.
  • Pfeiler, W. (2017): Experimentalphysik V: Quanten, Atome, Kerne, Teilchen. Berlin, Boston.
  • Steiner, R. (1920): Zweiter Naturwissenschaftlicher Kurs, GA 321, 12. Vortrag vom 12.3.1920, 5. Auflage. Dornach, 2021.
  • Voigt, W. (1898): Doppelbrechung von im Magnetfeld befindlichen Natriumdampf in der Richtung normal zu den Kraftlinien, Nachr. Kgl. Ges. Wiss. Göttingen, S. 355–359.
  • Wood, R.W. (1904): A Quantitative Determination of Anomalous Dis- persion of Sodium Vapour in the Visible and Ultra-Violet Regions, Proceedings of the American Academy of Arts and Sciences 40, S. 365–396.