Articles

Der Mensch und das Rätsel des Unendlichen – Mathematisches Denken zwischen Werden und Gewordenem

Uwe Hansen
Elemente der Naturwissenschaft 110, 2019, S. 79-91 | DOI: 10.18756/edn.110.79
Article | Sprache: German | €6.00
Artikelreferenz exportieren

Zusammenfassung:

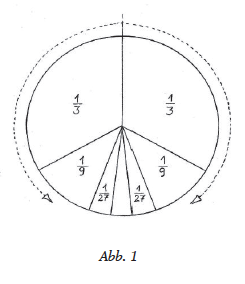
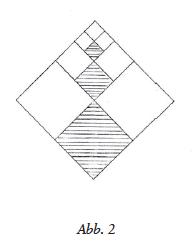
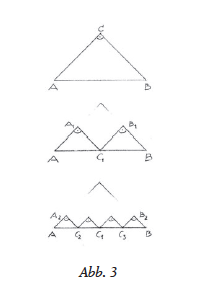
An einigen Beispielen aus Mathematik und Geometrie wird dargestellt, wie das Unendliche als Raum des Möglichen erscheint, wenn es als Prozess einer fortgesetzten gesetzmässigen Tätigkeit vorgestellt wird. Im Gegensatz dazu arbeitet die aktuale Auffassung des Unendlichen mit einer Menge mathematischer Objekte, die einerseits unendlich viele Teile beherbergt, andererseits im Ganzen als konstante Grösse gehandhabt wird. Wird das Unendliche im Unterricht über das innere Konstruieren einer geometrischen Figur eingeführt, die sich auf eine «Grenzfigur» zubewegt, ermöglicht dies dem Schüler das Erlebnis eines zwar subjektiv hervorgebrachten, aber doch gesetzmässig bestimmten Werdenden. Insofern dabei mathematische Gesetzmässigkeiten durch die innere Aktivität des Menschen in Erscheinung treten, wird verständlich, warum Rudolf Steiner das mathematische Tun als Musterbeispiel für eine übersinnliche Tätigkeit anführt. In dieser mathematischen Tätigkeit begegnen sich Geistiges und Physisches, sodass mathematisches Denken eine Brücke zum Geistigen bildet. Diese Brückenfunktion geht mit der Auffassung des Unendlichen als ein Aktual-Unendliches verloren. 

Referenzen
  • Bolzano, B. (1850): Paradoxien des Unendlichen, Prag.
  • Cantor, G. (1932): Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. Zermelo, E. (Hg.), Berlin.
  • Bedürftig, T., Murawski, R. (2015): Philosophie der Mathematik. Berlin.
  • Steiner, R. (1904): Aus dem Aufsatz «Mathematik und Okkultismus». Dor- nach 2014, GA 35.
  • Steiner, R. (1904): Spirituelle Seelenlehre und Weltbetrachtung. Vortrag vom 31.3.1904. Dornach 1986, GA 52.
  • Steiner, R. (1907): Natur- und Geistwesen. Ihr Wirken in unserer sichtbaren Welt. Vortrag vom 25.12.1907. Dornach 1983, GA 98.
  • Steiner, R. (1913): Das Leben zwischen Tod und neuer Geburt im Verhältnis zu den kosmischen Tatsachen. Vortrag vom 11.2.1913. Dornach 1997, GA 141.
  • Steiner, R. (1914): Das innere Wesen des Menschen und das Leben zwischen Tod und neuer Geburt. Vortrag vom 6.4.1914. Dornach 1997, GA 153.
  • Steiner, R. (1916): Die Verbindung zwischen Lebenden und Toten. Vortrag vom 22.2.1916. Dornach 1995, GA 168.
  • Steiner, R. (1916): Notwendigkeit und Freiheit im Weltgeschehen und im menschlichen Handeln. Vortrag vom 25.1.1916. Dornach 2018, GA 166.
  • Steiner, R. (1920): Die Brücke zwischen der Weltgeistigkeit und den Physischen des Menschen. Vortrag vom 19.12.1920. Dornach 1993, GA 202.
  • Steiner, R. (1920): Die Vierte Dimension. Fragenbeantwortung vom 15.10.1920. Dornach 1995, GA 324a.
  • Steiner, R. (1921): Mathematik, Wissenschaftliches Experiment, Beobachtung und Erkenntnisergebnisse vom Gesichtspunkt der Anthroposophie. Vortrag vom 16.3.1921. Dornach 1991, GA324.
  • Steiner, R. (1922): Damit der Mensch ganz Mensch werde. Vortrag vom 8.4.1922. Dornach 1994, GA 82.
  • Steiner, R. (1925): Wahrspruchworte. Zwölf Stimmungen, Spruch zu Wassermann. Dornach 1998, GA 40.
  • Steiner, R. (1995): Beiträge zur Gesamtausgabe Nr. 114/115. Rudolf Steiner Nachlassverwaltung (Hg.). Dornach.
  • Weizsäcker von, C.F. (1974): Die Einheit der Natur. München.