Articles

Der Mensch und das Rätsel des Unendlichen – Mathematisches Denken zwischen Werden und Gewordenem

Uwe Hansen
Elemente der Naturwissenschaft 110, 2019, P. 79-91 | DOI: 10.18756/edn.110.79
Article | Language: German | €6.00
Export Article Citation as

Abstract:

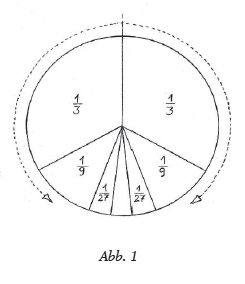
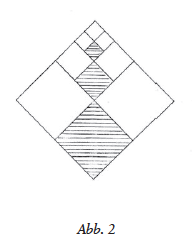
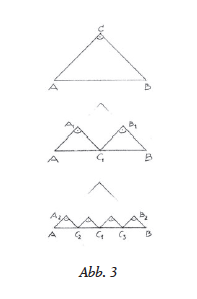
Some examples from mathematics and geometry illustrate how the infinite appears as a space of possibility when presented as a process of continued lawful activity. In contrast, the actual concept of infinity works with a set of mathematical objects, which on the one hand contains an infinity of subsets, on the other hand is handled as a constant quantity. If the infinite is introduced in teaching by requesting the inner construction of a geometric figure, which moves towards a “boundary figure”, this enables the student to experience a “becoming” that is subjectively produced, but nevertheless lawfully determined. Insofar as mathematical laws only appear through the inner activity of man it becomes clear why Rudolf Steiner takes mathematical thinking as a prime example of an imaginative inner experience . The spiritual and physical realm meet in this activity. Mathematical thinking thus forms a bridge to the spiritual world. This bridge character is lost with the understanding of the infinite as a finite actuality. 

References
  • Bolzano, B. (1850): Paradoxien des Unendlichen, Prag.
  • Cantor, G. (1932): Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. Zermelo, E. (Hg.), Berlin.
  • Bedürftig, T., Murawski, R. (2015): Philosophie der Mathematik. Berlin.
  • Steiner, R. (1904): Aus dem Aufsatz «Mathematik und Okkultismus». Dor- nach 2014, GA 35.
  • Steiner, R. (1904): Spirituelle Seelenlehre und Weltbetrachtung. Vortrag vom 31.3.1904. Dornach 1986, GA 52.
  • Steiner, R. (1907): Natur- und Geistwesen. Ihr Wirken in unserer sichtbaren Welt. Vortrag vom 25.12.1907. Dornach 1983, GA 98.
  • Steiner, R. (1913): Das Leben zwischen Tod und neuer Geburt im Verhältnis zu den kosmischen Tatsachen. Vortrag vom 11.2.1913. Dornach 1997, GA 141.
  • Steiner, R. (1914): Das innere Wesen des Menschen und das Leben zwischen Tod und neuer Geburt. Vortrag vom 6.4.1914. Dornach 1997, GA 153.
  • Steiner, R. (1916): Die Verbindung zwischen Lebenden und Toten. Vortrag vom 22.2.1916. Dornach 1995, GA 168.
  • Steiner, R. (1916): Notwendigkeit und Freiheit im Weltgeschehen und im menschlichen Handeln. Vortrag vom 25.1.1916. Dornach 2018, GA 166.
  • Steiner, R. (1920): Die Brücke zwischen der Weltgeistigkeit und den Physischen des Menschen. Vortrag vom 19.12.1920. Dornach 1993, GA 202.
  • Steiner, R. (1920): Die Vierte Dimension. Fragenbeantwortung vom 15.10.1920. Dornach 1995, GA 324a.
  • Steiner, R. (1921): Mathematik, Wissenschaftliches Experiment, Beobachtung und Erkenntnisergebnisse vom Gesichtspunkt der Anthroposophie. Vortrag vom 16.3.1921. Dornach 1991, GA324.
  • Steiner, R. (1922): Damit der Mensch ganz Mensch werde. Vortrag vom 8.4.1922. Dornach 1994, GA 82.
  • Steiner, R. (1925): Wahrspruchworte. Zwölf Stimmungen, Spruch zu Wassermann. Dornach 1998, GA 40.
  • Steiner, R. (1995): Beiträge zur Gesamtausgabe Nr. 114/115. Rudolf Steiner Nachlassverwaltung (Hg.). Dornach.
  • Weizsäcker von, C.F. (1974): Die Einheit der Natur. München.