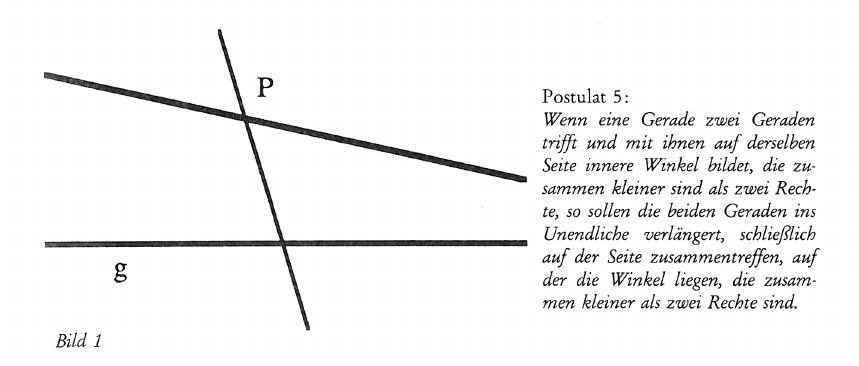
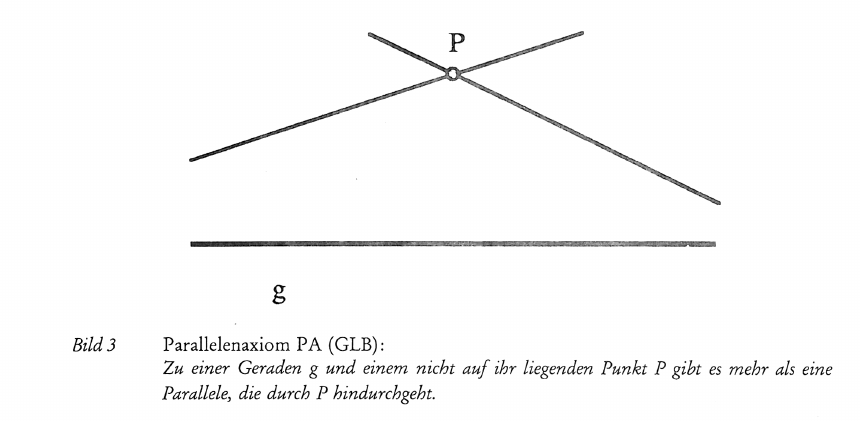
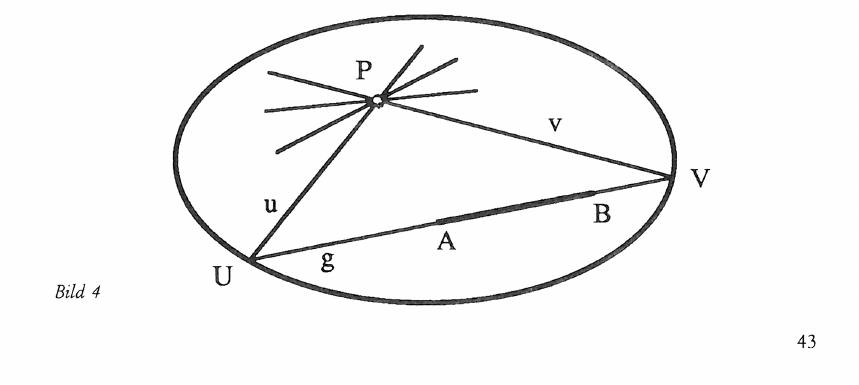
Die Entdeckung der nichteuklidischen Geometrien und ihre Folgen
Artikelreferenz exportieren
- Klartext
- BibTeX
- RIS Format
- Downloadkosten : € 6.00
Zusammenfassung:
Die Entdeckung der nichteuklidischen Geometrie gilt mit Recht als eine der einflußreichsten Errungenschaften des 19. Jahrhunderts. Die von ihr ausgehende Umgestaltung der Mathematik und schließlich der mathematischen Physik hatte tiefgehende Folgen für die Entwicklung des Weltbildes des Naturwissenschaftlers und Philosophen. Sogar die Künstler waren davon betroffen und inspiriert (siehe Henderson, 1983). Im vorliegenden Aufsatz möchte ich eine Facette aus diesem umfangreichen Komplex von sich ineinander verschlingenden und gegenseitig beeinflussenden Entwicklungsströmungen herausgreifen, die bewußtseinsgeschichtlich besonders aufschlußreich ist. Es handelt sich um die Bedeutung der Entdeckung der nichteuklidischen Geometrie für die Entwicklung des philosophischen Selbstverständnisses der mathematischen Methode in den Naturwissenschaften. [...]